What Is the Moment of Inertia of This Rod for an Axis at Its Center, Perpendicular to the Rod?

10 Fixed-Axis Rotation

10.5 Calculating Moments of Inertia

Learning Objectives

By the end of this section, you lot will be able to:

Summate the moment of inertia for uniformly shaped, rigid bodies
Apply the parallel centrality theorem to find the moment of inertia about any axis parallel to i already known
Calculate the moment of inertia for compound objects

In the preceding department, we defined the moment of inertia but did non show how to calculate it. In this section, we show how to calculate the moment of inertia for several standard types of objects, as well every bit how to use known moments of inertia to find the moment of inertia for a shifted centrality or for a compound object. This section is very useful for seeing how to use a general equation to complex objects (a skill that is critical for more than advanced physics and technology courses).

Moment of Inertia

Nosotros divers the moment of inertia I of an object to be

$I=\sum _{i}{m}_{i}{r}_{i}^{2}$

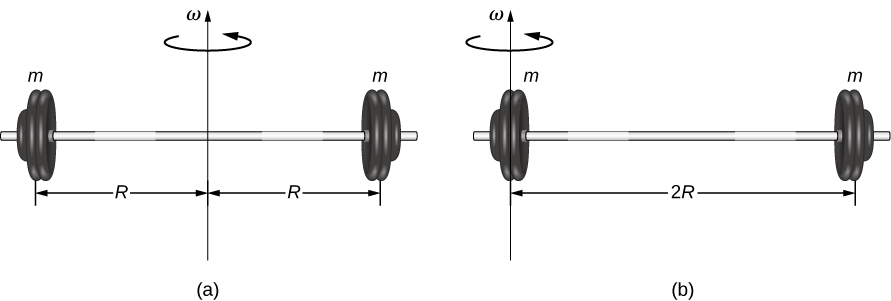
for all the signal masses that brand upward the object. Because r is the altitude to the axis of rotation from each piece of mass that makes up the object, the moment of inertia for any object depends on the chosen axis. To see this, let's have a simple instance of ii masses at the terminate of a massless (negligibly small mass) rod ((Effigy)) and calculate the moment of inertia about two different axes. In this case, the summation over the masses is uncomplicated because the two masses at the stop of the barbell tin exist approximated as bespeak masses, and the sum therefore has but ii terms.
In the case with the centrality in the center of the barbell, each of the 2 masses m is a distance R away from the centrality, giving a moment of inertia of

${I}_{1}=m{R}^{2}+m{R}^{2}=2m{R}^{2}.$

In the case with the axis at the end of the barbell—passing through 1 of the masses—the moment of inertia is

${I}_{2}=m{(0)}^{2}+m{(2R)}^{2}=4m{R}^{2}.$

From this result, we can conclude that it is twice as hard to rotate the barbell about the end than nearly its eye.

Figure A shows a barbell of the length 2 R with the masses m at the ends. It is rotating through its center. Figure B shows a barbell of the length 2 R with the masses m at the ends. It is rotating through one end. — **Figure 10.23** (a) A barbell with an axis of rotation through its center; (b) a barbell with an axis of rotation through i end.

In this example, nosotros had 2 point masses and the sum was uncomplicated to summate. However, to bargain with objects that are not bespeak-like, we need to call up carefully about each of the terms in the equation. The equation asks u.s.a. to sum over each 'piece of mass' a sure altitude from the axis of rotation. But what exactly does each 'piece of mass' mean? Recall that in our derivation of this equation, each piece of mass had the aforementioned magnitude of velocity, which ways the whole piece had to have a single distance r to the axis of rotation. However, this is not possible unless we take an infinitesimally small piece of mass dm, every bit shown in (Effigy).

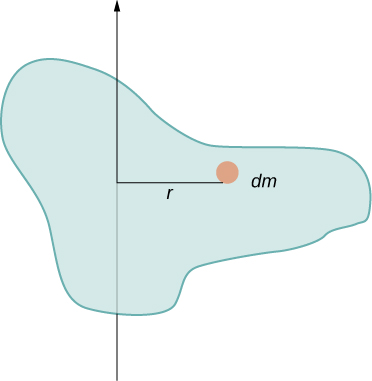
Figure shows a point dm located on the X axis at distance r from the center. — **Figure x.24** Using an infinitesimally minor piece of mass to summate the contribution to the total moment of inertia.

The need to use an infinitesimally minor piece of mass dm suggests that nosotros can write the moment of inertia by evaluating an integral over minute masses rather than doing a discrete sum over finite masses:

$I=\sum _{i}{m}_{i}{r}_{i}{}^{2}\enspace\text{becomes}I=\int {r}^{2}dm.$

This, in fact, is the form we need to generalize the equation for complex shapes. It is best to work out specific examples in detail to go a feel for how to calculate the moment of inertia for specific shapes. This is the focus of most of the rest of this department.

A uniform sparse rod with an axis through the center

Consider a uniform (density and shape) thin rod of mass M and length L as shown in (Figure). We desire a thin rod so that we can assume the cross-exclusive area of the rod is small and the rod can be thought of as a string of masses along a one-dimensional straight line. In this example, the centrality of rotation is perpendicular to the rod and passes through the midpoint for simplicity. Our task is to summate the moment of inertia about this centrality. We orient the axes and then that the z-centrality is the centrality of rotation and the ten-centrality passes through the length of the rod, as shown in the figure. This is a convenient selection because we can then integrate along the x-axis.

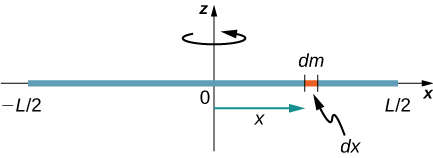
Figure shows a thin rod that rotates about an axis through the center. Part of the rod of the length dx has a mass dm. — **Figure 10.25** Calculation of the moment of inertia I for a compatible thin rod well-nigh an axis through the center of the rod.

We define dm to be a small element of mass making up the rod. The moment of inertia integral is an integral over the mass distribution. However, we know how to integrate over space, not over mass. We therefore need to find a style to chronicle mass to spatial variables. Nosotros practice this using the linear mass density

$\lambda$

of the object, which is the mass per unit length. Since the mass density of this object is uniform, we tin write

$\lambda =\frac{m}{l}\enspace\text{or}m=\lambda l.$

If nosotros take the differential of each side of this equation, we find

$dm=d(\lambda l)=\lambda (dl)$

since

$\lambda$

is constant. We chose to orient the rod along the x-axis for convenience—this is where that selection becomes very helpful. Note that a slice of the rod dl lies completely along the ten-axis and has a length dx; in fact,

$dl=dx$

in this situation. We can therefore write

$dm=\lambda (dx)$

, giving us an integration variable that nosotros know how to bargain with. The distance of each slice of mass dm from the axis is given past the variable x, as shown in the effigy. Putting this all together, we obtain

$I=\int {r}^{2}dm=\int {x}^{2}dm=\int {x}^{2}\lambda dx.$

The last step is to exist careful about our limits of integration. The rod extends from

$x=\text{−}L\text{/}2$

$x=L\text{/}2$

, since the centrality is in the middle of the rod at

$x=0$

. This gives us

$\begin{array}{cc}\hfill I& =\underset{\text{−}L\text{/}2}{\overset{L\text{/}2}{\int }}{x}^{2}\lambda dx=\lambda \frac{{x}^{3}}{3}{|}_{\text{−}L\text{/}2}^{L\text{/}2}=\lambda (\frac{1}{3})[{(\frac{L}{2})}^{3}-{(\frac{\text{−}L}{2})}^{3}]\hfill \\ & =\lambda (\frac{1}{3})\frac{{L}^{3}}{8}(2)=\frac{M}{L}(\frac{1}{3})\frac{{L}^{3}}{8}(2)=\frac{1}{12}M{L}^{2}.\hfill \end{array}$

Side by side, nosotros calculate the moment of inertia for the aforementioned uniform sparse rod but with a dissimilar axis pick so we tin can compare the results. Nosotros would await the moment of inertia to be smaller nearly an axis through the center of mass than the endpoint centrality, but as it was for the barbell example at the kickoff of this department. This happens because more mass is distributed farther from the centrality of rotation.

A uniform thin rod with axis at the end

At present consider the aforementioned uniform thin rod of mass M and length L, just this time we motion the centrality of rotation to the end of the rod. We wish to ﬁnd the moment of inertia well-nigh this new centrality ((Figure)). The quantity dm is once again defined to be a pocket-size element of mass making upwards the rod. But as earlier, we obtain

$I=\int {r}^{2}dm=\int {x}^{2}dm=\int {x}^{2}\lambda dx.$

However, this time we have different limits of integration. The rod extends from

$x=0$

$x=L$

, since the axis is at the end of the rod at

$x=0$

. Therefore we find

$\begin{array}{cc}\hfill I& =\underset{0}{\overset{L}{\int }}{x}^{2}\lambda dx=\lambda \frac{{x}^{3}}{3}{|}_{0}^{L}=\lambda (\frac{1}{3})[{(L)}^{3}-{(0)}^{3}]\hfill \\ & =\lambda (\frac{1}{3}){L}^{3}=\frac{M}{L}(\frac{1}{3}){L}^{3}=\frac{1}{3}M{L}^{2}.\hfill \end{array}$

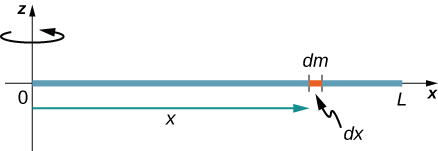
Figure shows a thin rod that rotates about an axis through the end. Part of the rod of the length dx has a mass dm. — **Figure x.26** Calculation of the moment of inertia I for a compatible thin rod about an centrality through the terminate of the rod.

Note the rotational inertia of the rod about its endpoint is larger than the rotational inertia nigh its center (consequent with the barbell example) by a gene of 4.

The Parallel-Axis Theorem

The similarity between the process of finding the moment of inertia of a rod about an axis through its centre and nearly an axis through its cease is striking, and suggests that at that place might exist a simpler method for determining the moment of inertia for a rod virtually any axis parallel to the axis through the center of mass. Such an axis is called a parallel axis. There is a theorem for this, chosen the parallel-axis theorem, which we country here but do non derive in this text.

Parallel-Axis Theorem

Let m be the mass of an object and let d exist the distance from an axis through the object's center of mass to a new axis. Then we have

${I}_{\text{parallel-axis}}={I}_{\text{center of mass}}+m{d}^{2}.$

Let's utilise this to the rod examples solved higher up:

${I}_{\text{end}}={I}_{\text{center of mass}}+m{d}^{2}=\frac{1}{12}m{L}^{2}+m{(\frac{L}{2})}^{2}=(\frac{1}{12}+\frac{1}{4})m{L}^{2}=\frac{1}{3}m{L}^{2}.$

This result agrees with our more than lengthy calculation from higher up. This is a useful equation that we apply in some of the examples and bug.

Check Your Understanding

What is the moment of inertia of a cylinder of radius R and mass k almost an axis through a bespeak on the surface, as shown beneath?

Figure shows a cylinder of radius R that rotates about an axis through a point on the surface.

[reveal-answer q="530534″]Show Answer[/reveal-answer]
[hidden-answer a="530534″]

${I}_{\text{parallel-axis}}={I}_{\text{center of mass}}+m{d}^{2}=m{R}^{2}+m{R}^{2}=2m{R}^{2}$

[/hidden-reply]

A compatible thin deejay well-nigh an axis through the center

Integrating to discover the moment of inertia of a ii-dimensional object is a little bit trickier, merely one shape is ordinarily done at this level of report—a compatible thin deejay about an centrality through its center ((Figure)).

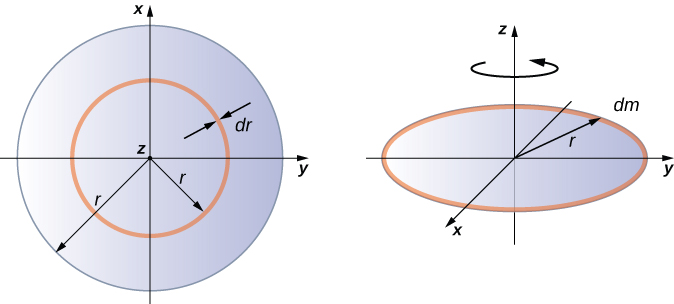
Figure shows a uniform thin disk of radius r that rotates about a Z axis that passes through its center. — **Figure 10.27** Computing the moment of inertia for a thin disk near an centrality through its heart.

Since the deejay is thin, we can take the mass every bit distributed entirely in the xy-plane. We once again starting time with the relationship for the surface mass density, which is the mass per unit surface expanse. Since it is uniform, the surface mass density

$\sigma$

is abiding:

$\sigma =\frac{m}{A}\quad \text{or}\quad \sigma A=m,\,\text{so}\,dm=\sigma (dA).$

Now we use a simplification for the expanse. The area can exist idea of equally fabricated up of a serial of sparse rings, where each ring is a mass increment dm of radius r equidistanct from the centrality, as shown in function (b) of the figure. The minute expanse of each ring dA is therefore given by the length of each ring (

$2\pi r$

) times the infinitesimmal width of each ring dr:

$A=\pi {r}^{2},dA=d(\pi {r}^{2})=\pi d{r}^{2}=2\pi rdr.$

The full area of the disk is then made up from adding all the thin rings with a radius range from 0 to R. This radius range and then becomes our limits of integration for dr, that is, nosotros integrate from

$r=0$

$r=R$

. Putting this all together, we have

$\begin{array}{cc}\hfill I& =\underset{0}{\overset{R}{\int }}{r}^{2}\sigma (2\pi r)dr=2\pi \sigma \underset{0}{\overset{R}{\int }}{r}^{3}dr=2\pi \sigma \frac{{r}^{4}}{4}{|}_{0}^{R}=2\pi \sigma (\frac{{R}^{4}}{4}-0)\hfill \\ & =2\pi \frac{m}{A}(\frac{{R}^{4}}{4})=2\pi \frac{m}{\pi {R}^{2}}(\frac{{R}^{4}}{4})=\frac{1}{2}m{R}^{2}.\hfill \end{array}$

Notation that this agrees with the value given in (Effigy).

Computing the moment of inertia for compound objects

At present consider a compound object such every bit that in (Effigy), which depicts a thin disk at the finish of a thin rod. This cannot be easily integrated to notice the moment of inertia because it is not a uniformly shaped object. All the same, if we go back to the initial definition of moment of inertia as a summation, nosotros can reason that a compound object'southward moment of inertia can be establish from the sum of each part of the object:

${I}_{\text{total}}=\sum _{i}{I}_{i}.$

Information technology is of import to annotation that the moments of inertia of the objects in (Figure) are near a common axis. In the example of this object, that would be a rod of length L rotating virtually its end, and a thin disk of radius R rotating about an axis shifted off of the eye by a altitude

$L+R$

, where R is the radius of the disk. Permit's ascertain the mass of the rod to be

${m}_{\text{r}}$

and the mass of the disk to be

${m}_{\text{d}}.$

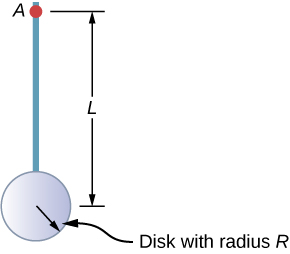
Figure shows a disk with radius R connected to a rod with length L. — **Figure 10.28** Compound object consisting of a disk at the cease of a rod. The axis of rotation is located at A.

The moment of inertia of the rod is merely

$\frac{1}{3}{m}_{\text{r}}{L}^{2}$

, but we have to utilize the parallel-axis theorem to find the moment of inertia of the deejay about the centrality shown. The moment of inertia of the disk well-nigh its center is

$\frac{1}{2}{m}_{\text{d}}{R}^{2}$

and we apply the parallel-axis theorem

${I}_{\text{parallel-axis}}={I}_{\text{center of mass}}+m{d}^{2}$

to find

${I}_{\text{parallel-axis}}=\frac{1}{2}{m}_{\text{d}}{R}^{2}+{m}_{\text{d}}{(L+R)}^{2}.$

Adding the moment of inertia of the rod plus the moment of inertia of the disk with a shifted centrality of rotation, nosotros discover the moment of inertia for the chemical compound object to be

${I}_{\text{total}}=\frac{1}{3}{m}_{\text{r}}{L}^{2}+\frac{1}{2}{m}_{\text{d}}{R}^{2}+{m}_{\text{d}}{(L+R)}^{2}.$

Applying moment of inertia calculations to solve problems

Now let's examine some practical applications of moment of inertia calculations.

Instance

Person on a Merry-Become-Round

A 25-kg child stands at a distance

$r=1.0\,\text{m}$

from the axis of a rotating merry-become-circular ((Figure)). The merry-go-round can exist approximated every bit a uniform solid deejay with a mass of 500 kg and a radius of two.0 grand. Find the moment of inertia of this organization.

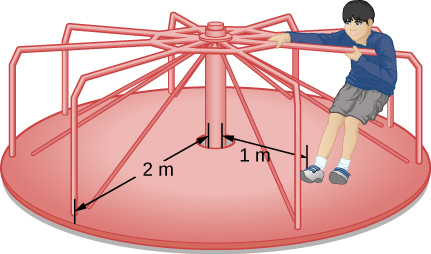
Figure is a drawing of a child on a merry-go-round. Merry–go-round has a 2 meter radius. Child is standing one meter from the center. — **Figure 10.29** Calculating the moment of inertia for a child on a merry-go-round.

Strategy

This problem involves the calculation of a moment of inertia. Nosotros are given the mass and distance to the axis of rotation of the child besides as the mass and radius of the merry-go-circular. Since the mass and size of the child are much smaller than the merry-go-round, we can gauge the child as a point mass. The notation nosotros use is

${m}_{\text{c}}=25\,\text{kg},{r}_{\text{c}}=1.0\,\text{m},{m}_{\text{m}}=500\,\text{kg},{r}_{\text{m}}=2.0\,\text{m}$

Our goal is to find

${I}_{\text{total}}=\sum _{i}{I}_{i}$

Solution

For the child,

${I}_{\text{c}}={m}_{\text{c}}{r}^{2}$

, and for the merry-get-round,

${I}_{\text{m}}=\frac{1}{2}{m}_{\text{m}}{r}^{2}$

. Therefore

${I}_{\text{total}}=25{(1)}^{2}+\frac{1}{2}(500){(2)}^{2}=25+1000=1025\,\text{kg}·{\text{m}}^{2}.$

Significance

The value should be close to the moment of inertia of the merry-get-round by itself because it has much more mass distributed away from the axis than the child does.

Example

Rod and Solid Sphere

Find the moment of inertia of the rod and solid sphere combination about the two axes as shown below. The rod has length 0.5 m and mass 2.0 kg. The radius of the sphere is 20.0 cm and has mass ane.0 kg.

Figure A shows a disk with radius R connected to a rod with length L. The point A is at the end of the rod opposite to the disk. Figure B shows a disk with radius R connected to a rod with length L. The point B is at the end of the rod connected to the disk.

Strategy

Since we have a compound object in both cases, we tin use the parallel-centrality theorem to find the moment of inertia well-nigh each axis. In (a), the center of mass of the sphere is located at a altitude

$L+R$

from the centrality of rotation. In (b), the heart of mass of the sphere is located a distance R from the axis of rotation. In both cases, the moment of inertia of the rod is nigh an axis at one end. Refer to (Figure) for the moments of inertia for the individual objects.

${I}_{\text{total}}=\sum _{i}{I}_{i}={I}_{\text{Rod}}+{I}_{\text{Sphere}}$

;

${I}_{\text{Sphere}}={I}_{\text{center of mass}}+{m}_{\text{Sphere}}{(L+R)}^{2}=\frac{2}{5}{m}_{\text{Sphere}}{R}^{2}+{m}_{\text{Sphere}}{(L+R)}^{2}$

;

${I}_{\text{total}}={I}_{\text{Rod}}+{I}_{\text{Sphere}}=\frac{1}{3}{m}_{\text{Rod}}{L}^{2}+\frac{2}{5}{m}_{\text{Sphere}}{R}^{2}+{m}_{\text{Sphere}}{(L+R)}^{2};$

${I}_{\text{total}}=\frac{1}{3}(2.0\,\text{kg}){(0.5\,\text{m})}^{2}+\frac{2}{5}(1.0\,\text{kg})(0.2\,{\text{m})}^{2}+(1.0\,\text{kg}){(0.5\,\text{m}+0.2\,\text{m})}^{2};$

${I}_{\text{total}}=(0.167+0.016+0.490)\,\text{kg}·{\text{m}}^{2}=0.673\,\text{kg}·{\text{m}}^{2}.$
${I}_{\text{Sphere}}=\frac{2}{5}{m}_{\text{Sphere}}{R}^{2}+{m}_{\text{Sphere}}{R}^{2}$

;

${I}_{\text{total}}={I}_{\text{Rod}}+{I}_{\text{Sphere}}=\frac{1}{3}{m}_{\text{Rod}}{L}^{2}+\frac{2}{5}{m}_{\text{Sphere}}{R}^{2}+{m}_{\text{Sphere}}{R}^{2}$

;

${I}_{\text{total}}=\frac{1}{3}(2.0\,\text{kg}){(0.5\,\text{m})}^{2}+\frac{2}{5}(1.0\,\text{kg})(0.2\,{\text{m})}^{2}+(1.0\,\text{kg}){(0.2\,\text{m})}^{2}$

;

${I}_{\text{total}}=(0.167+0.016+0.04)\,\text{kg}·{\text{m}}^{2}=0.223\,\text{kg}·{\text{m}}^{2}.$

Significance

Using the parallel-axis theorem eases the ciphering of the moment of inertia of compound objects. We run across that the moment of inertia is greater in (a) than (b). This is considering the axis of rotation is closer to the center of mass of the system in (b). The uncomplicated analogy is that of a rod. The moment of inertia about i end is

$\frac{1}{3}m{L}^{2}$

, only the moment of inertia through the center of mass forth its length is

$\frac{1}{12}m{L}^{2}$

Instance

Angular Velocity of a Pendulum

A pendulum in the shape of a rod ((Effigy)) is released from residual at an angle of

$30\text{°}$

. Information technology has a length 30 cm and mass 300 one thousand. What is its angular velocity at its lowest point?

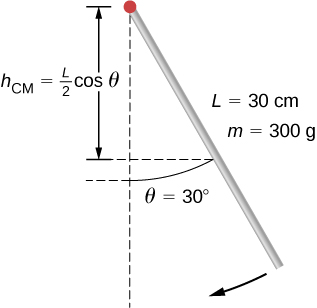
Figure shows a pendulum in the form of a rod with a mass of 300 grams and length of 30 centimeters. Pendulum is released from rest at an angle of 30 degrees. — **Effigy 10.30** A pendulum in the form of a rod is released from residuum at an angle of
$30\text{°}.$

Strategy

Use conservation of energy to solve the problem. At the signal of release, the pendulum has gravitational potential energy, which is determined from the height of the center of mass to a higher place its everyman bespeak in the swing. At the bottom of the swing, all of the gravitational potential free energy is converted into rotational kinetic free energy.

Solution

The modify in potential free energy is equal to the change in rotational kinetic free energy,

$\Delta U+\Delta K=0$

At the superlative of the swing:

$U=mg{h}_{\text{cm}}=mg\frac{L}{2}(\text{cos}\,\theta )$

. At the bottom of the swing,

$U=mg\frac{L}{2}.$

At the meridian of the swing, the rotational kinetic energy is

$K=0$

. At the bottom of the swing,

$K=\frac{1}{2}I{\omega }^{2}$

. Therefore:

$\text{Δ}U+\text{Δ}K=0⇒(mg\frac{L}{2}(1-\text{cos}\,\theta )-0)+(0-\frac{1}{2}I{\omega }^{2})=0$

$\frac{1}{2}I{\omega }^{2}=mg\frac{L}{2}(1-\text{cos}\,\theta ).$

Solving for

$\omega$

, we have

$\omega =\sqrt{mg\frac{L}{I}(1-\text{cos}\,\theta )}=\sqrt{mg\frac{L}{1\text{/}3m{L}^{2}}(1-\text{cos}\,\theta )}=\sqrt{g\frac{3}{L}(1-\text{cos}\,\theta )}.$

Inserting numerical values, we have

$\omega =\sqrt{9.8\,\text{m}\text{/}{\text{s}}^{2}\frac{3}{0.3\,\text{m}}(1-\text{cos}\,30)}=3.6\,\text{rad}\text{/}\text{s}.$

Significance

Annotation that the angular velocity of the pendulum does not depend on its mass.

Summary

Moments of inertia tin can exist found by summing or integrating over every 'piece of mass' that makes up an object, multiplied past the square of the altitude of each 'piece of mass' to the axis. In integral form the moment of inertia is
$I=\int {r}^{2}dm$

.
Moment of inertia is larger when an object's mass is farther from the axis of rotation.
It is possible to find the moment of inertia of an object virtually a new centrality of rotation one time it is known for a parallel axis. This is called the parallel axis theorem given by
${I}_{\text{parallel-axis}}={I}_{\text{center of mass}}+m{d}^{2}$

, where d is the distance from the initial centrality to the parallel centrality.
Moment of inertia for a chemical compound object is just the sum of the moments of inertia for each individual object that makes upward the chemical compound object.

Conceptual Questions

If a kid walks toward the center of a merry-go-round, does the moment of inertia increase or decrease?

A discus thrower rotates with a discus in his hand earlier letting it go. (a) How does his moment of inertia change after releasing the discus? (b) What would be a expert approximation to use in calculating the moment of inertia of the discus thrower and discus?

[reveal-reply q="fs-id1167133845959″]Prove Solution[/reveal-reply]

[hidden-answer a="fs-id1167133845959″]

a. It decreases. b. The arms could be approximated with rods and the discus with a deejay. The trunk is most the centrality of rotation so it doesn't contribute much to the moment of inertia.

[/hidden-reply]

Does increasing the number of blades on a propeller increase or decrease its moment of inertia, and why?

The moment of inertia of a long rod spun around an axis through one cease perpendicular to its length is

$m{L}^{2}\text{/}3$

. Why is this moment of inertia greater than information technology would exist if you spun a betoken mass grand at the location of the center of mass of the rod (at L/two) (that would exist

$m{L}^{2}\text{/}4$

[reveal-answer q="fs-id1167133354662″]Show Solution[/reveal-answer]

[hidden-reply a="fs-id1167133354662″]

Considering the moment of inertia varies every bit the foursquare of the altitude to the axis of rotation. The mass of the rod located at distances greater than L/ii would provide the larger contribution to make its moment of inertia greater than the indicate mass at L/2.

[/hidden-answer]

Why is the moment of inertia of a hoop that has a mass M and a radius R greater than the moment of inertia of a disk that has the same mass and radius?

Issues

While punting a football, a kicker rotates his leg virtually the hip joint. The moment of inertia of the leg is

$3.75{\,\text{kg-m}}^{2}$

and its rotational kinetic energy is 175 J. (a) What is the angular velocity of the leg? (b) What is the velocity of tip of the punter's shoe if it is 1.05 yard from the hip joint?

Using the parallel axis theorem, what is the moment of inertia of the rod of mass k nigh the axis shown below?

Figure shows a rod that rotates around the axis that passes through it at 1/6 of length from one end and 5/6 of length from the opposite end.

[reveal-answer q="96051″]Prove Reply[/reveal-answer]
[hidden-respond a="96051″]

$I=\frac{7}{36}m{L}^{2}$

[/subconscious-answer]

Find the moment of inertia of the rod in the previous problem by direct integration.

A compatible rod of mass ane.0 kg and length 2.0 m is costless to rotate about one stop (see the post-obit figure). If the rod is released from residual at an angle of

$60\text{°}$

with respect to the horizontal, what is the speed of the tip of the rod as it passes the horizontal position?
Figure shows a rod that is released from rest at an angle of 60 degrees with respect to the horizontal.

[reveal-answer q="71295″]Show Answer[/reveal-answer]
[hidden-reply a="71295″]

$v=7.14\,\text{m}\text{/}\text{s}.$

[/subconscious-answer]

A pendulum consists of a rod of mass two kg and length 1 m with a solid sphere at one end with mass 0.iii kg and radius 20 cm (run into the following figure). If the pendulum is released from rest at an angle of

$30\text{°}$

, what is the angular velocity at the lowest point?
Figure shows a pendulum that consists of a rod of mass 2 kg and length 1 m with a solid sphere at one end with mass 0.3 kg and radius 20 cm. The pendulum is released from rest at an angle of 30 degrees.

A solid sphere of radius x cm is allowed to rotate freely most an axis. The sphere is given a sharp blow so that its center of mass starts from the position shown in the post-obit figure with speed 15 cm/s. What is the maximum angle that the diameter makes with the vertical?

Left figure shows a solid sphere of radius 10 cm that first rotates freely about an axis and then received a sharp blow in its center of mass. Right figure is the image of the same sphere after the blow. An angle that the diameter makes with the vertical is marked as theta.

[reveal-answer q="602090″]Prove Answer[/reveal-answer]
[hidden-answer a="602090″]

$\theta =10.2\text{°}$

[/hidden-answer]

Calculate the moment of inertia by direct integration of a thin rod of mass Yard and length Fifty about an axis through the rod at L/3, as shown below. Check your answer with the parallel-axis theorem.

Figure shows a rod that rotates around the axis that passes through it at 1/3 of length from one end and 2/3 of length from the opposite end.

Glossary

linear mass density

the mass per unit length

$\lambda$

of a one dimensional object

parallel centrality: axis of rotation that is parallel to an axis about which the moment of inertia of an object is known

parallel-axis theorem: if the moment of inertia is known for a given axis, it tin be found for any axis parallel to it

surface mass density

mass per unit of measurement surface area

$\sigma$

of a ii dimensional object

brownbeirme.blogspot.com

Source: https://opentextbc.ca/universityphysicsv1openstax/chapter/10-5-calculating-moments-of-inertia/

What Is the Moment of Inertia of This Rod for an Axis at Its Center, Perpendicular to the Rod?

10.5 Calculating Moments of Inertia

Learning Objectives

Moment of Inertia

A uniform sparse rod with an axis through the center

A uniform thin rod with axis at the end

The Parallel-Axis Theorem

Parallel-Axis Theorem

Check Your Understanding

A compatible thin deejay well-nigh an axis through the center

Computing the moment of inertia for compound objects

Applying moment of inertia calculations to solve problems

Instance

Person on a Merry-Become-Round

Strategy

Solution

Significance

Example

Rod and Solid Sphere

Strategy

Significance

Instance

Angular Velocity of a Pendulum

Strategy

Solution

Significance

Summary

Conceptual Questions

Issues

Glossary

0 Response to "What Is the Moment of Inertia of This Rod for an Axis at Its Center, Perpendicular to the Rod?"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel